Magnets Database PMAG
Magnetic Properties of all Hard Magnetic Materials (Permanent Magnet Materials, e.g. Neodymium, Samarium Cobalt, Ferrite etc.)

Magnetic Materials: Powering Modern Technologies
Magnetic materials are the backbone of countless modern technologies. They power massive utility generators, drive compact electric motors in vehicles, and play an essential role in converting electrical energy into mechanical energy—and vice versa. However, during this conversion, all magnetic materials produce heat. Choosing the wrong material can result in excessive heat buildup, reducing efficiency and shortening the machine’s lifespan. This is why selecting magnetic materials with minimal heat dissipation is critical to developing high magnetic efficiency.
Efficiency Parameters
Magnetic Efficiency is controlled by the Magnetic Property Curves
Not all magnetic materials are equally efficient. Some dissipate heat more, some less. Their magnetic efficiency is measured by two curves:
- Magnetization Curves: These show how magnetic flux density B [tesla] changes with magnetic field strength H [ampere/meter].
- Core Loss Curves:These show how heat dissipation P [watt/kg] changes with flux density B [tesla].
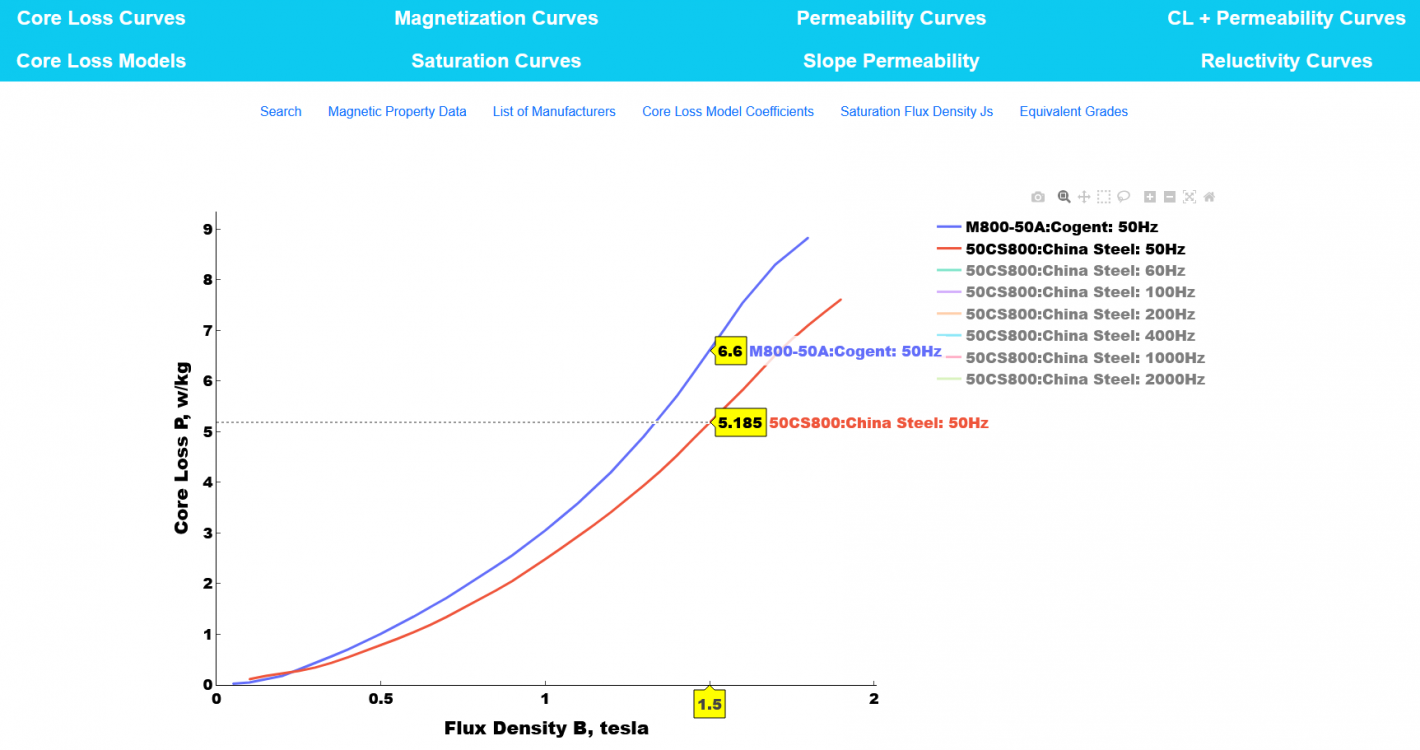

The Challenge of Material Selection
Countless Grades are produced by manufacturers worldwide, each made by their specific process. Selecting the best magnetic material out of this immense choice is highly complex. To determine an optimal magnetic material, you need to study the trade-off between umpteen factors that affect heat dissipation – like the Manufacturer, Grade, lamination thickness, grain orientation, annealing, field strength, flux density, frequency, and temperature. Determining the magnetic material with the lowest heat loss thus requires complex and time-consuming analysis—this is where MagWeb comes in.
MagWeb's Solution
MagWeb streamlines the magnetic material selection process through its comprehensive magnetic property database and innovative visualization tools. Our database contains thousands of Magnetization and Core Loss curves from global manufacturers. Unfortunately, their raw data is not always smooth, and may not converge when used in Finite Element Analysis software such as Maxwell and COMSOL. We process all this raw data with proprietary smoothing algorithms to ensure fast, converging results. Our data and Visualizers also extend to Saturation Magnetization, so that you can test your machine when it is oversaturated.

Visualizing Magnetic Properties
Our web-based Visualizers present this data in interactive graphical form, making it easy to compare material grades side-by-side. Features like a movable cursor allow precise evaluation of core losses, enabling you to choose the most efficient magnetic material for your application.
Power in Your Hands - For Free
Selecting the right magnetic material can transform your machine’s performance. MagWeb’s Visualizers let you explore how different parameters affect efficiency—quickly, clearly, and confidently. For a limited time, we are offering free access to these powerful tools so you can streamline your material selection process and achieve optimal results.
Help MagWeb Grow - Donate Now
Custom Need?
Interested in magnetic property database for specific magnetic materials (e.g., stainless steel or carbon steel)? Please fill 'Contact us' form under Resources, or email to: rao@magweb.us
